Freeverb3 - Calculating the frequency response of a digital filter

The newest version of the freeverb3 library includes log sweep generator, which can be used to calculate the frequency reponse of the digital filters. The sample code is in the source package.

You should use double precision instead of single precision to calculate them since the error is too large in some situations.

Initialize Log Sweep Class

#include <freeverb/sweep.hpp>
typedef double pfloat_t;
typedef fv3::sweep_ SWEEP;
SWEEP S;
S.setCurrentFs(48000);
S.setStartFs(0.001);
S.setEndFs(23000);
S.setInitialMuteLength(100);
S.setSweepLength(100);
S.setLeadInLength(0);
S.setLeadOutLength(0);
S.setEndMuteLength(100);
S.init();
long totalLength = S.getTotalLength();
fprintf(stderr, "SweepLength = %ld\n", totalLength);

Generate Log Sweep and calculate filter

  pfloat_t *forward1, *forward2, *inverse, *mute, *out1, *out2;
  forward1 = new pfloat_t[totalLength];
  forward2 = new pfloat_t[totalLength];
  mute = new pfloat_t[totalLength];
  UTILS::mute(mute, totalLength);
  inverse = new pfloat_t[totalLength];
  out1 = new pfloat_t[totalLength*2];
  out2 = new pfloat_t[totalLength*2];

  DELAY DD;
  long dsize = 24;
  DD.setsize(dsize);
  
  for(long l = 0;l < totalLength;l++)
    {
      pfloat_t input = S.process(1);
      pfloat_t output = input+0.9*DD.getlast();
      DD.process(output);
      forward1[l] = output;
      forward2[l] = input;
    }

Generate InverseLog Sweep and calculate FFT

  std::cerr << "Inverse Log Sweep Calculation..." << std::endl;
  IRMODEL3 FIR;
  S.setInverseMode(true); S.init();
  for(long l = 0;l < totalLength;l++){ inverse[l] = S.process(1); }
  FIR.setwetr(1); FIR.setdryr(0);
  FIR.loadImpulse(inverse,inverse,totalLength);
  
  std::cerr << "Inverse Log Sweep Convolution Calculation..." << std::endl;
  FIR.processreplace(forward1,forward2,out1,out2,totalLength,FV3_IR_MUTE_DRY|FV3_IR_SKIP_FILTER);
  FIR.processreplace(mute,mute,out1+totalLength,out2+totalLength,totalLength,FV3_IR_MUTE_DRY|FV3_IR_SKIP_FILTER);

  std::cerr << "Impulse FFT Calculation..." << std::endl;
  FFTW_(plan) p, q;
  p = FFTW_(plan_r2r_1d)(totalLength*2, out1, out1, FFTW_R2HC, FFTW_ESTIMATE);
  q = FFTW_(plan_r2r_1d)(totalLength*2, out2, out2, FFTW_R2HC, FFTW_ESTIMATE);
  FFTW_(execute)(p); FFTW_(execute)(q);
  FFTW_(destroy_plan)(p); FFTW_(destroy_plan)(q);

Calculate the magnitude and the phase

  forward1[0] = std::sqrt(out1[0]*out1[0]+out1[totalLength]*out1[totalLength]) /
    std::sqrt(out2[0]*out2[0]+out2[totalLength]*out2[totalLength]);
  forward2[0] = 0;
  for(long l = 1;l < (totalLength-1);l ++)
    {
      // amplitude
      forward1[l] =
	std::sqrt(out1[l]*out1[l]+out1[totalLength*2-l]*out1[totalLength*2-l]) /
	std::sqrt(out2[l]*out2[l]+out2[totalLength*2-l]*out2[totalLength*2-l]);
      // phase
      forward2[l] =
	std::atan2(out1[totalLength*2-l],out1[l]) - std::atan2(out2[totalLength*2-l],out2[l]);
      if(forward2[l] > M_PI)      forward2[l] -= 2*M_PI;
      if(forward2[l] < M_PI*(-1)) forward2[l] += 2*M_PI;
    }
  for(long l = 0;l < (totalLength-1);l ++)
    {
      printf("%ld %f %f\n", l, forward1[l], forward2[l]);
    }

Output example

0 10.000002 0.000000
1 9.987687 -0.047083
2 9.951015 -0.093922
3 9.890785 -0.140281
4 9.808273 -0.185938
5 9.705163 -0.230687
6 9.583456 -0.274350
7 9.445363 -0.316773
8 9.293220 -0.357831
9 9.129384 -0.397428
...
14389 8.775723 0.471981
14390 8.956143 0.435492
14391 9.129364 0.397427
14392 9.293199 0.357830
14393 9.445354 0.316771
14394 9.583450 0.274348
14395 9.705168 0.230685
14396 9.808286 0.185936
14397 9.890811 0.140281
14398 9.951032 0.093922

GNUPLOT graph examples

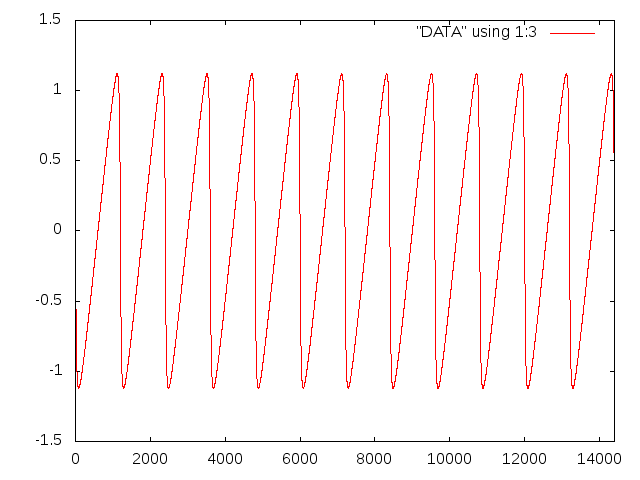
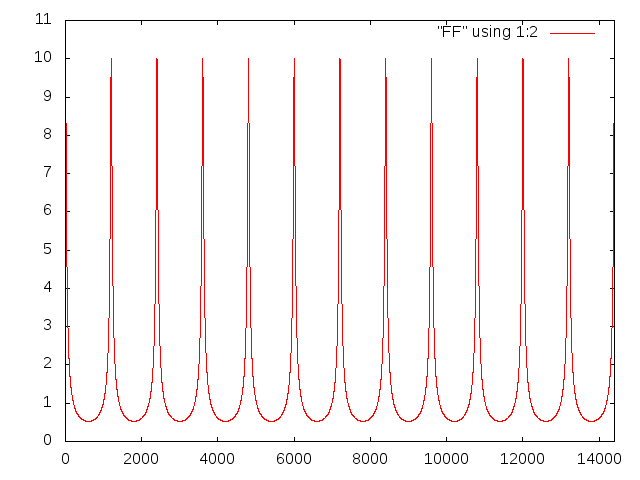
gnuplot> # Plot Frequency Response
gnuplot> plot [:14400] "DATA" using 1:2 w l
gnuplot> # Plot Phase Change
gnuplot> plot [:14400] "DATA" using 1:3 w l

Calculating the frequency response of a digital filter